Being familiar with the standards vertically K-5 provides the big picture of how each grade level’s requirements work together to help students develop a deep understanding of fractions. Below we have compiled understanding fractions K-5 teaching resources.

Here is a round-up of simple, standards-aligned ideas and resources to support understanding fraction concepts, models, and computations. Basically, students will use manipulatives, drawings, or numbers to represent and compute varied fraction skills in their math careers from grades K-5.

Grades K-2

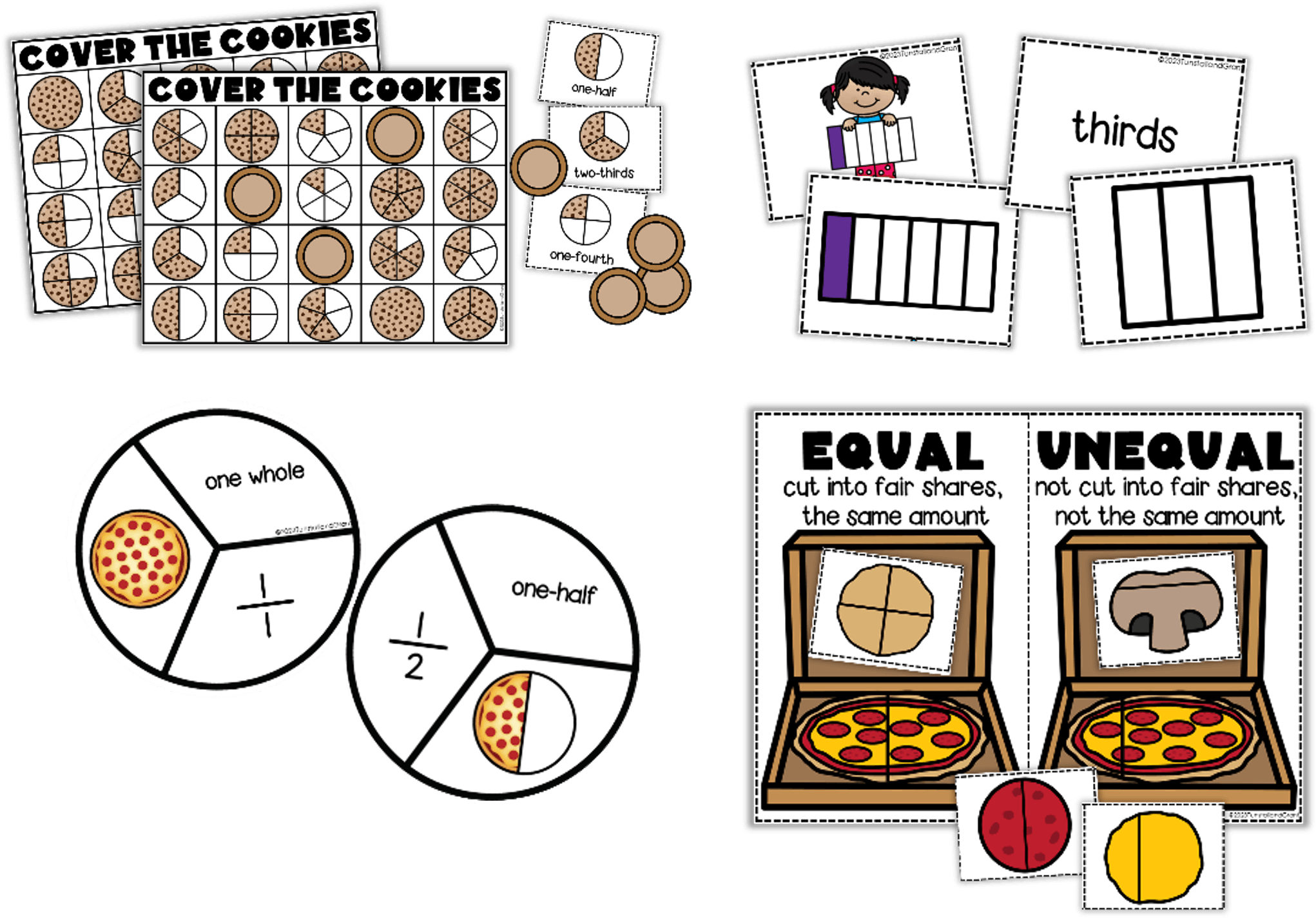
While Kindergarten doesn’t explicitly have fractions standards, we lead students in seeing how we can compose larger shapes from smaller shapes. Students in this grade level usually identify equal or unequal halves (of food!) in the real world through experiences.

In the same way, in grades one and up, students begin partitioning whole shapes into parts, halves, and quarters, identifying equal and non-equal shapes, and composing and decomposing shapes into two and four equal shares.

Grade 2 is where we begin to address fractions formally. We continue partitioning objects and naming parts, including thirds and eighths (depending on where you live). Second grade is where we write fractions in word form. We understand and explain that the more fractional parts used to make a whole, the smaller the part; the fewer the fractional parts, the larger the part. We can also grasp that equal shares of identical wholes can have different shapes. For example, a rectangle is cut into four equal columns or four equal squares.

Grades 3-5

Equally, grade three begins our steep uphill climb of representing, comparing, and finding equivalent fractions. This is where we want to be sure to provide hands-on exploration explicitly. While students can identify fractions from the younger grades, the understanding is likely not rich with connecting visually, creating a representation, or understanding how it might translate from a fraction model to a number line.

To continue, Grade 4 we add in adding and subtracting fractions with like denominators and comparing fractions with unlike denominators. Multiplying fractions by whole numbers and generating equivalent fractions means that students will need visual models, work mats, and plenty of practice with different fraction tools.

Moving up, in Grade 5, students apply their understanding of fractions and fraction models to represent the addition and subtraction of fractions with unlike denominators. At this level, students develop fluency in calculating sums and differences of fractions and make reasonable estimates of them.

Finally, it is no secret that fractions are an f-word to many adults, and likely, this is due to a lack of real understanding. We can equip students to have a better understanding of the ‘whole’ idea, from the beginning to the end!